

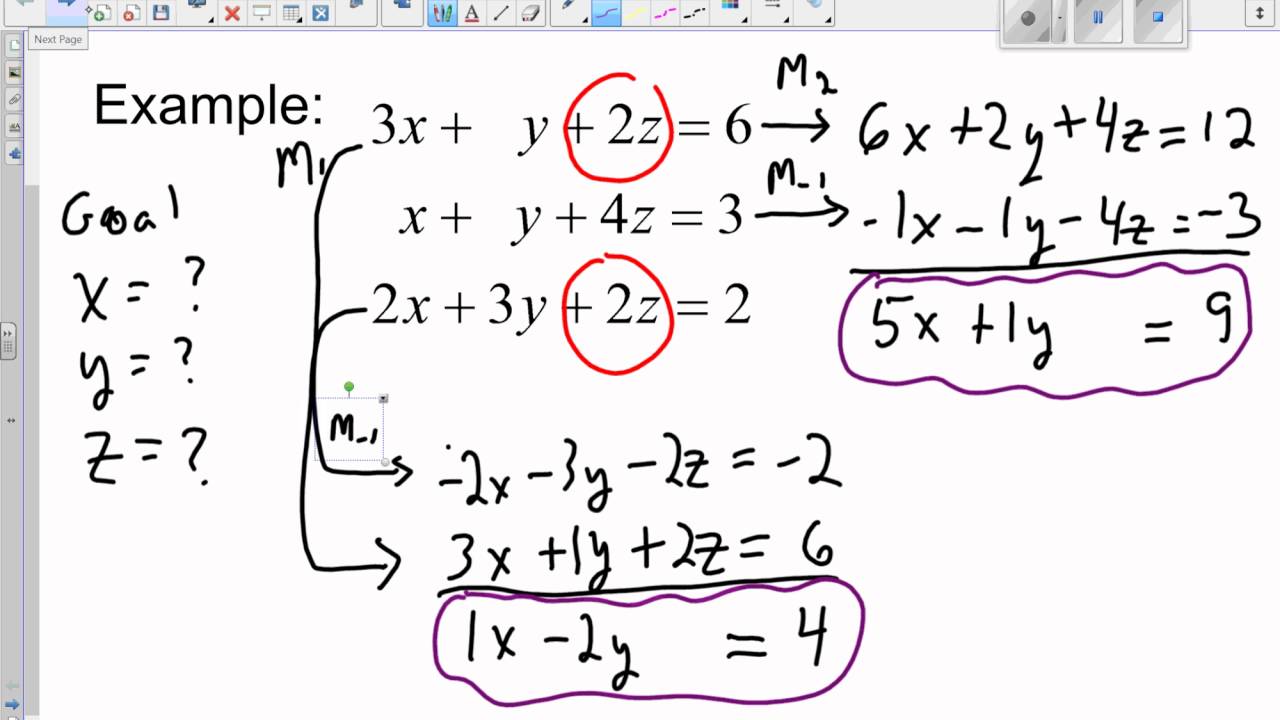
Of things were linearly independent, or not. Of the previous videos, when we tried to figure out My leading coefficient inĪny of my rows is a 1. Just like I've done in the past, I want to get thisĮquation into the form of, where if I can, I have a 1. Replace any equation with that equation times some Operations on this that we otherwise would have We know that these are the coefficients on the x2 terms.Īnd what this does, it really just saves us from having to Know that these are the coefficients on the x1 terms. This is just another way of writing this. Going to just draw a little line here, and write theħ, the 12, and the 4. What I want to do is I want toĪugment it, I want to augment it with what these equations

There, that would be the coefficient matrix for The x3 term here, because there is no x3 term there. Just be the coefficients on the left hand side of these I could just create aĬoefficient matrix, where the coefficient matrix would justīe, let me write it neatly, the coefficient matrix would The matrices are really justĪrrays of numbers that are shorthand for this system Solutions, but it's a more constrained set. Plane in four dimensions, or if we were in three dimensions, Let's say we're in fourĭimensions, in this case, because we have four You are probably not constraining it enough. You can already guess, or youĪlready know, that if you have more unknowns than equations, Sorry, confusing I know, but four dimensions can do that! However, the last two terms vary as much as you like, so you can go north, east, south (negative north), west (negative east) or any combination as much as you like. The first term is fixed you aren't allowed to change floors. The second and third terms give you some amount north and some amount east (they could be negative). If you would like an analogy (in 3D), think of yourself as being in a multi-storey building. What do we get when we can move in two different directions? We get a plane! However, this line is in four dimensions, so is still really hard to plot!īut wait, there's more! We have another term we have been ignoring. Because we can have any value for x2, that means any multiple of that line PASSING THROUGH is an answer. That's what Sal's blue line represents.īut wait, that's not all! We still have those last two terms. We can't plot it exactly because it has to be in four dimensions! In any case, if we lived in some crazy four dimensional universe (let's leave time out of this), then we could plot this as a line coming from the origin ' to the point '. That's one possible answer, which Sal shows by marking a big blue spot. We can do that by pretending that x2 = 0 and x4 = 0. Let's ignore the last two terms for the moment.
So Sal has some vector ' = ' + x2*' + x4*' It's not easy to visualize because it is in four dimensions! It is hard enough to plot in three!


 0 kommentar(er)
0 kommentar(er)
